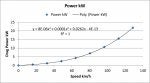
Ich habe die beigefügte Tabelle entwickelt, die die gesamte Schleppleistung (kW) im Vergleich zur Geschwindigkeit (km/h) des Ioniq EV zeigt.
Die Tabelle basiert auf der offiziellen EPA-Veröffentlichung der Luftwiderstandsbeiwerte für den Ioniq EV.
Die EPA verwendet Koeffizienten für die Funktion y=Cx^2+Bx+A, wobei y der gesamte Luftwiderstand (Widerstand) in lbf und x die Geschwindigkeit in mph ist.
Die Zielkoeffizienten für den Ioniq EV, die von der EPA ermittelt (oder von Hyundai an die EPA übermittelt) wurden, sind: Koeffizient A=21,17(lbf) Koeffizient B=0,19016(lbf/mph) und Koeffizient C=0,015762(lbf/mph^2).
Die Tabelle basiert auf der offiziellen EPA-Veröffentlichung der Luftwiderstandsbeiwerte für den Ioniq EV.
Die EPA verwendet Koeffizienten für die Funktion y=Cx^2+Bx+A, wobei y der gesamte Luftwiderstand (Widerstand) in lbf und x die Geschwindigkeit in mph ist.
Die Zielkoeffizienten für den Ioniq EV, die von der EPA ermittelt (oder von Hyundai an die EPA übermittelt) wurden, sind: Koeffizient A=21,17(lbf) Koeffizient B=0,19016(lbf/mph) und Koeffizient C=0,015762(lbf/mph^2).